A satisfying proof
In 1777, Georges-Louis Leclerc, Comte de Buffon posed the following question:
Suppose we have a floor made of parallel wooden boards, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two boards?
He solved it with some fancy calculus, which is a fine way of doing it, but not particularly satisfying to me. However in 1860 a man named Joseph-Émile Barbier came up with this super slick proof, which is without a doubt the coolest proof I've ever seen.
The trick is that rather than trying to calculate the probability directly, Barbier examined it through the lens of the expected number of lines the needle would cross.
Suppose we define our boards to be 1 unit of distance wide, and we find that dropping a needle of length 1 unit has a probability $p$ of crossing one of the lines. We will ignore the possibility of the needle being exactly along a line, or having one end each on precisely two lines, since the probability of those is 0.
If we drop one needle $n_1$, our expected number of crossings is simply $p$, the probability that the needle crosses a line.
If we drop a second needle $n_2$, then by linearity of expectation we find that our expected total number of crossings is
$$E(n_1+n_2)=E(n_1)+E(n_2)=2p$$
In general, the expected number of crossings when you drop $m$ needles is $mp$.
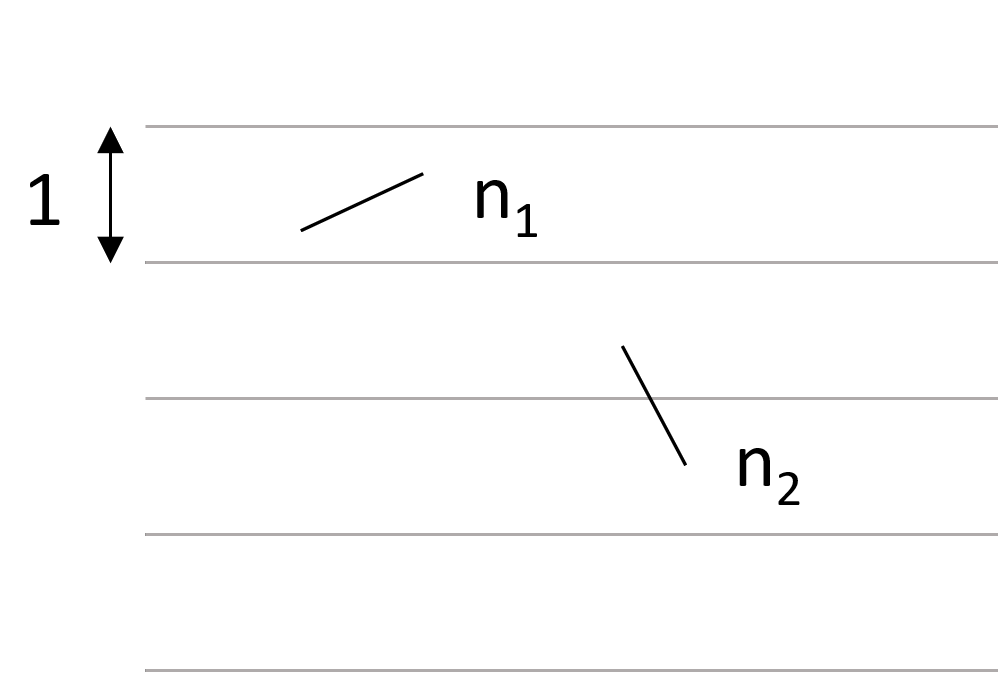
Figure 1: Two needles on the floor
Similarly, if we drop a needle $n$ and break it into $m$ identical pieces $n_1 \ldots n_m$ we find that each piece must be responsible for the same expected number of crossings:
$$E(n) = \sum_{i=0}^{m}E(n_i) \implies E(n_i)=\frac{1}{p}$$
In short, we can drop a needle of any length $\ell$ we want and the expected number of crossings will be $\ell p$. This holds even if we drop some really bizarre needles:
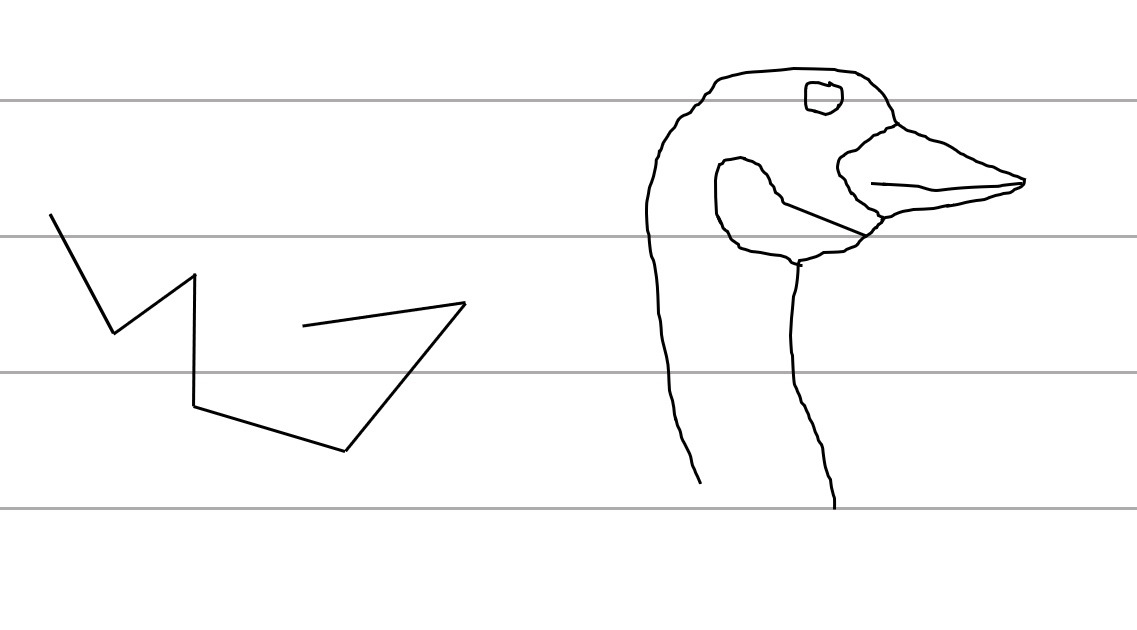
Figure 2: Some strangely shaped needles indeed
Now suppose we take a needle and bend it into a circle of diameter 1. We know that the expected number of crossings must be $\pi p$ from before. But consider the ways the needle could fall on the floor:
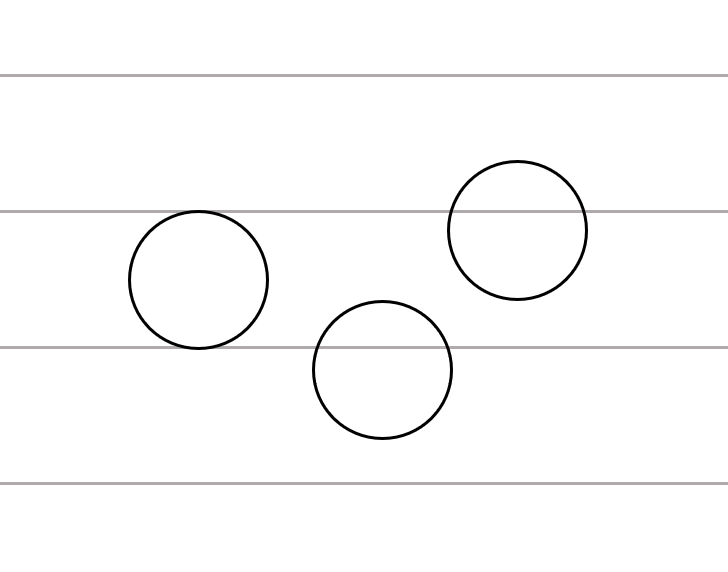
Figure 3: Three needles, bent into circles
It always crosses in exactly two places! So $\pi p=2$ and we find that $p=\frac{2}{\pi}$. Any straight needle we drop on the floor will have probability $\frac{2\ell}{\pi}$ of crossing a line. And we didn't do a single bit of calculus!